DeepLeaning AI Multi Object Tracker

基于 sort 算法的多目标跟踪

Posted by feizaipp on March 9, 2021

我的博客

1. 概述

       本文介绍基于 Sort 算法的多目标跟踪方案，实现车流量统计。该方案主要由三个部分组成。 yolov3 进行目标检测、使用匈牙利算法对目标进行关联、使用卡尔曼滤波器对跟踪目标进行修正。

2. yolov3 模型的使用

       之前的文章中介绍过 yolov3 模型，这里不在进行赘述，本文使用 opencv 内部提供的 yolov3 接口进行实现，这里介绍下 yolov3 的 opencv 接口。

       在 opencv 的 dnn 模块中包含了主流的深度学习模型，但要注意只提供推理功能，不支持模型训练。

2.1. yolov3 模型的应用

       加载 yolov3 模型：

  • readNetFromDarknet: 参数 1 指定网络的配置信息，参数 2 指定模型的预训练权重。 
    weightsPath = "./yolo-coco/yoloV3.weights"
configPath = "./yolo-coco/yoloV3.cfg"
net = cv2.dnn.readNetFromDarknet(configPath, weightsPath)

       获取网络输出层。

  • getLayerNames: 获取所有网络层的名称。
  • getUnconnectedOutLayers: 获取网络输出层的索引。
  • ln: 保存 yolov3 网络输出层，分别是 [yolo-82,yolo-94,yolo-106] 
    ln = net.getLayerNames()
ln = [ln[i[0] - 1] for i in net.getUnconnectedOutLayers()]

       使用 opencv 接口获取视频流，并送入 yolov3 网络进行目标检测。

  • blobFromImage: dnn 接口，对图像进行加载并进行预处理。
  • net.forward: 将图像输入进网络，并进行前向传播，返回 yolov3 3 个层的目标预测结果。
  • 遍历每一个输出层，遍历每一个预测结果，筛选 confidence > 0.3 的预测结果
  • boxes: 保存预测边界框的中心点坐标和宽高
  • confidences: 保存置信度
  • classIDs: 保存类别 id
  • NMSBoxes: 对上面进行筛选过后的预测信息通过非极大值抑制算法再进行筛选，其中 0.5 是 score_threshold ； 0.3 是 nms_threshold 。该函数返回符合要求的边界框的索引。
  • 遍历经过非极大值抑制处理后的边界框，因为我们做车流量统计，只保留检测类别是车的边界框，将符合要求的边界框的左上角坐标和右下角坐标和置信度保存到 dets 中 
    vs = cv2.VideoCapture('./input/test_1.mp4')
(W, H) = (None, None)
writer = None
while True:
  (grabed, frame) = vs.read()
  if W is None or H is None:
      (H,W) = frame.shape[:2]
  blob = cv2.dnn.blobFromImage(frame, 1 / 255.0, (416, 416), swapRB=True, crop=False)
  net.setInput(blob)
  layerOutputs = net.forward(ln)
  boxes = []
  confidences = []
  classIDs = []
  for output in layerOutputs:
      for detection in output:
          # detction: [5:]: 表示类别，[0:4]: bbox 的位置信息， [4]: 置信度
          scores = detection[5:]
          classID = np.argmax(scores)
          confidence = scores[classID]

          if confidence > 0.3:
              # 将检测结果与原图片进行适配
              box = detection[0:4] * np.array([W, H, W, H])
              (centerX, centerY, width, height) = box.astype("int")
              # 左上角坐标
              x = int(centerX - width / 2)
              y = int(centerY - height / 2)
              # 更新目标框，置信度，类别
              boxes.append([x, y, int(width), int(height)])
              confidences.append(float(confidence))
              classIDs.append(classID)
  idxs = cv2.dnn.NMSBoxes(boxes, confidences, 0.5, 0.3)
  # 检测框:左上角和右下角
  dets = []
  if len(idxs) > 0:
      for i in idxs.flatten():
          if LABELS[classIDs[i]] == "car":
              (x, y) = (boxes[i][0], boxes[i][1])
              (w, h) = (boxes[i][2], boxes[i][3])
              # cv2.rectangle(frame,(x,y),(x+w,y+h),(0,255,0),2)
              dets.append([x, y, x + w, y + h, confidences[i]])

3. 匈牙利算法

       匈牙利算法 (Hungarian Algorithm) 与 KM 算法 (Kuhn-Munkres Algorithm) 是用来解决多目标跟踪中的数据关联问题，匈牙利算法与 KM 算法都是为了求解二分图的最大匹配问题。

       那什么是二分图呢？就是能分成两组 U 和 V ，其中， U 上的点不能相互连通，只能连接 V 中的点，同理， V 中的点不能相互连通，只能连去 U 中的点，这就是做二分图。

       可以把二分图理解为视频中连续两帧中的所有检测框，第一帧所有检测框的集合称为 U ，第二帧所有检测框的集合称为 V 。同一帧的不同检测框不会为同一个目标，所以不需要互相关联，相邻两帧的检测框需要相互联通，最终将相邻两帧的检测框尽量完美地两两匹配起来。而求解这个问题的最优解就要用到匈牙利算法或者 KM 算法。

       匈牙利算法和 KM 算法的原理这里就不在赘述了，相关的资料网上多的是，这里我们只需要知道他们是干什么的就可以了。其中 KM 算法是匈牙利算法的改进版本，它解决的是带权二分图的最优匹配问题。在多目标跟踪中目标关联是根据前一帧数据与后一帧数据的 IOU 作为权值进行关联的。

       在 scipy 包中，通过 linear_sum_assignment 函数实现 KM 算法。

  • 构造代价矩阵 cost
  • 注意：传入 linear_sum_assignment 函数的代价矩阵要取负数。因为该方法的目的是代价最小，这里是求最大匹配，所以将 cost 取负数。 ``` from scipy.optimize import linear_sum_assignment import numpy as np

cost = np.array([[0.9,0.6,0,0],[0,0.3,0.9,0],[0.5,0.9,0,0],[0,0,0.2,0]]) row_ind,col_ind = linear_sum_assignment(-cost)


# 4.卡尔曼滤波
       卡尔曼滤波无论是在单目标还是多目标领域都是很常用的一种算法，我们将卡尔曼滤波看做一种运动模型，用来对目标的位置进行预测，并且利用预测结果对跟踪的目标进行修正，属于自动控制理论中的一种方法。

       在对视频中的目标进行跟踪时，当目标运动速度较慢时，很容易将前后两帧的目标进行关联，如下图所示:

![](/img/Kalman1.png)

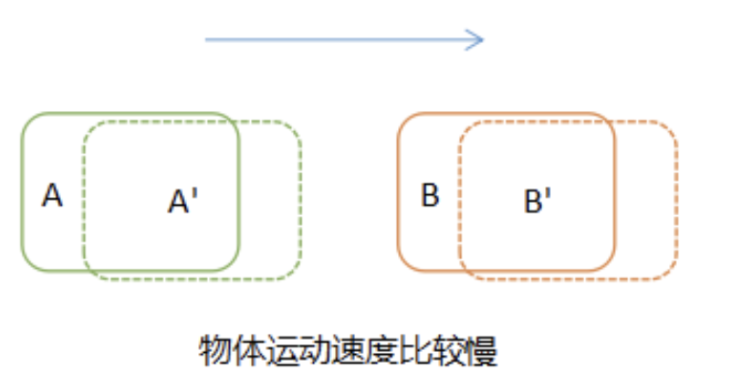
       如果目标运动速度比较快，或者进行隔帧检测时，在后续帧中，目标A已运动到前一帧B所在的位置，这时再进行关联就会得到错误的结果，将 A' 与 B 关联在一起。

       那怎么才能避免这种出现关联误差呢？我们可以在进行目标关联之前，对目标在后续帧中出现的位置进行预测，然后与预测结果进行对比关联，如下图所示：

![](/img/Kalman2.png)

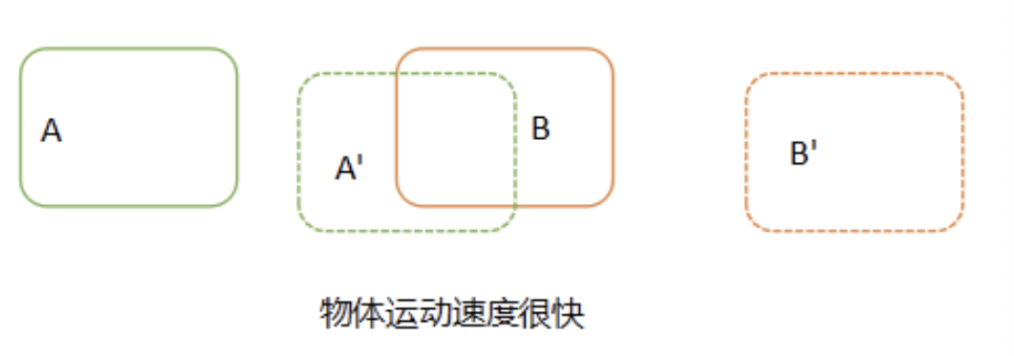
       我们在对比关联之前，先预测出 A 和 B 在下一帧中的位置，然后再使用实际的检测位置与预测的位置进行对比关联，只要预测足够精确，几乎不会出现由于速度太快而关联错误的情况。

       卡尔曼滤波就是用来预测目标在后续帧中出现的位置。卡尔曼滤波器最大的优点是采用递归的方法来解决线性滤波的问题，它只需要当前的测量值和前一个周期的预测值就能够进行状态估计。由于这种递归方法不需要大量的存储空间，每一步的计算量小，计算步骤清晰，非常适合计算机处理，因此卡尔曼滤波受到了普遍的欢迎，在各种领域具有广泛的应用前景。

       简单理解卡尔曼滤波分为两步，预测和更新。预测是根据上一周期的预测值对当前状进行估计。更新是用当前的观测值更新卡尔曼滤波器，用于下次状态的估计，这实际上就是递归。更新阶段是卡尔曼滤波的数据融合，它融合了估计值和观测值的结果，充分利用两者的不确定性来得到更加准确的估计。

       以上就是卡尔曼滤波的简单思想，如果想了解详细的推理过程可以自行搜集资料进行研究。

       在实际使用卡尔曼滤波的时候，计算的步骤一般为：
* 预测阶段

![](/img/Kalman3.png)

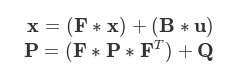
* 更新阶段

![](/img/Kalman4.png)

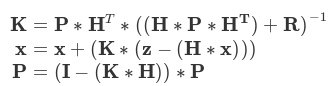
# 4.1. 卡尔曼滤波器的实现
       卡尔曼滤波器的实现在 filterpy 包里。 filterpy 是一个实现了各种滤波器的 Python 模块，它实现著名的卡尔曼滤波和粒子滤波器。我们可以直接调用该库完成卡尔曼滤波器实现。

from filterpy.kalman import KalmanFilter


       定义一个卡尔曼滤波器用于跟踪目标边界框，上面已经提到了，卡尔曼的两大功能是预测和更新，该类中主要实现这两个接口。首先我们需要对滤波器进行初始化。

* 初始化卡尔曼滤波器的状态变量和观测输入，这里我们假设车的运动是一个等速模型。
* 状态变量 x 设定为一个七维向量， x = [u,v,s,r,u',v',s'].T ，分别表示目标中心位置的 x,y 坐标，面积 s 和当前目标框的纵横比，最后三个则是横向，纵向，面积的变化速率，其中速度部分初始化为 0 ，其他根据观测进行输入。
* 量测矩阵 H 是 4*7 的矩阵，将观测值与状态变量相对应。
* 根据经验值进行相应的协方差参数的设定 P Q R

class KalmanBoxTracker(object): count = 0

def __init__(self, bbox):
    # 定义等速模型
    # 内部使用KalmanFilter，7个状态变量和4个观测输入
    self.kf = KalmanFilter(dim_x=7, dim_z=4)
    # F是状态变换模型
    self.kf.F = np.array(
        [[1, 0, 0, 0, 1, 0, 0], [0, 1, 0, 0, 0, 1, 0], [0, 0, 1, 0, 0, 0, 1], [0, 0, 0, 1, 0, 0, 0],
         [0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 0, 0, 1]])
    # H是观测函数
    self.kf.H = np.array(
        [[1, 0, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0]])
    # R是观测函数
    self.kf.R[2:, 2:] *= 10.
    # P是协方差矩阵
    self.kf.P[4:, 4:] *= 1000.  # give high uncertainty to the unobservable initial velocities
    self.kf.P *= 10.
    # Q是过程噪声矩阵
    self.kf.Q[-1, -1] *= 0.01
    self.kf.Q[4:, 4:] *= 0.01
    # 内部状态估计
    self.kf.x[:4] = convert_bbox_to_z(bbox)
    self.time_since_update = 0
    self.id = KalmanBoxTracker.count
    KalmanBoxTracker.count += 1
    self.history = []
    self.hits = 0
    self.hit_streak = 0
    self.age = 0 ```

       使用观测值更新状态变量。

  • time_since_update: 该变量用于记录当前卡尔曼滤波器跟踪的目标有多少次未被跟踪到，当超过指定次数后，将该目标从跟踪列表中删除。每次 update 被调用时将该变量清零。
  • hit_streak: 该变量用于记录当前卡尔曼滤波器跟踪的目标被成功跟踪了多少次，当超过一定次数后，认为该目标跟踪成功 
    def update(self, bbox):
  self.time_since_update = 0
  self.history = []
  self.hits += 1
  self.hit_streak += 1
  self.kf.update(convert_bbox_to_z(bbox))

       使用前一状态对当前状太进行估计。

  • time_since_update: 该变量用于记录当前卡尔曼滤波器跟踪的目标有多少次未被跟踪到，当超过指定次数后，将该目标从跟踪列表中删除。每次 predict 被调用时将该变量加 1 。
  • hit_streak: 该变量用于记录当前卡尔曼滤波器跟踪的目标被成功跟踪了多少次，当超过一定次数后，认为该目标跟踪成功，当有一次为跟踪到时，将该变量置 0 。 
    def predict(self):
  if (self.kf.x[6] + self.kf.x[2]) <= 0:
      self.kf.x[6] *= 0.0
  self.kf.predict()
  self.age += 1
  if self.time_since_update > 0:
      self.hit_streak = 0
  self.time_since_update += 1
  self.history.append(convert_x_to_bbox(self.kf.x))
  return self.history[-1]

       返回当前估计值。

def get_state(self):
    return convert_x_to_bbox(self.kf.x)

5. Sort 算法实现

       Sort 算法实际上是一个多目标跟踪器，管理多个 KalmanBoxTracker 对象。

       首先我们看 Sort 类的构造方法。

  • max_age: 目标未被检测到的帧数，超过之后会被删除
  • min_hits: 目标连续被检测到 min_hits 次才对目标进行跟踪 
    class Sort(object):
  def __init__(self, max_age=1, min_hits=3):
      self.max_age = max_age
      self.min_hits = min_hits
      self.trackers = []   # ？
      self.frame_count = 0  # ？

       update 方法是 Sort 算法的核心，它实现了对目标的跟踪。

  • dets: 输入 yolov3 网络检测到的目标边界框
  • self.frame_count: 记录视频帧数
  • trks: 存储跟踪器的预测，根据当前所有的卡尔曼跟踪器个数创建二维数组，行号为卡尔曼滤波器的标识索引，列向量为跟踪框的位置和 ID ，当第一次开始检测时 self.trackers 的长度是 0
  • to_del: 存储要删除的目标框
  • ret: 存储要返回的追踪目标框
  • 循环遍历卡尔曼跟踪器列表，如果是第一次开始检测不会进入 for 循环。首先使用卡尔曼滤波器预测目标当前的位置，并把预测值保存到 trks 数组中，如果跟踪框中包含空值则将该跟踪框添加到要删除的列表中。
  • 将 trks 中存在无效值的行删除
  • 逆向删除异常的跟踪器，防止破坏索引
  • 将目标检测框与卡尔曼滤波器预测的跟踪框关联获取跟踪成功的目标，新增的目标，离开画面的目标。
  • 用跟踪成功的目标框更新到对应的卡尔曼滤波器，实际上就是之前提到的用观测值更新卡尔曼滤波器。
  • 为新增的目标创建新的卡尔曼滤波器对象进行跟踪。并将卡尔曼滤波器添加到 self.trackers 中。
  • 反向遍历卡尔曼滤波器列表，获取每一个卡尔曼滤波器的估计值，判断跟踪目标是否成功，成功则添加到列表中。判断是否跟踪成功的条件是连续 self.min_hits 次都跟踪到该目标。如果超过 self.max_age 次未跟踪到目标则认为该目标离开画面，删除对应的卡尔曼滤波器。
  • 最终将跟踪结果拼接到一起返回。 
    def update(self, dets):
  self.frame_count += 1
  trks = np.zeros((len(self.trackers), 5))
  to_del = []
  ret = []
  for t, trk in enumerate(trks):
      pos = self.trackers[t].predict()[0]
      trk[:] = [pos[0], pos[1], pos[2], pos[3], 0]
      if np.any(np.isnan(pos)):
          to_del.append(t)
  trks = np.ma.compress_rows(np.ma.masked_invalid(trks))
  for t in reversed(to_del):
      self.trackers.pop(t)
  matched, unmatched_dets, unmatched_trks = associate_detections_to_trackers(dets, trks)

  for t, trk in enumerate(self.trackers):
      if t not in unmatched_trks:
          d = matched[np.where(matched[:, 1] == t)[0], 0]
          trk.update(dets[d, :][0])

  for i in unmatched_dets:
      trk = KalmanBoxTracker(dets[i, :])
      self.trackers.append(trk)

  i = len(self.trackers)
  for trk in reversed(self.trackers):
      d = trk.get_state()[0]
      if (trk.time_since_update < 1) and (trk.hit_streak >= self.min_hits or self.frame_count <= self.min_hits):
          ret.append(np.concatenate((d, [trk.id + 1])).reshape(1, -1))
      i -= 1
      if trk.time_since_update > self.max_age:
          self.trackers.pop(i)
  if len(ret) > 0:
      return np.concatenate(ret)
  return np.empty((0, 5))

       在目标跟踪中，需要使用 KM 算法将卡尔曼滤波器估计的边界框与 yolov3 模型检测的边界框进行关联。

  • detections: 表示 yolov3 模型检测的边界框
  • trackers: 卡尔曼滤波器跟踪的边界框
  • iou_threshold: iou 阈值，该阈值用来判断估计模型与检测模型的匹配程度。
  • 函数返回跟踪成功目标的矩阵: matchs ；新增目标的矩阵: unmatched_detections ；跟踪失败即离开画面的目标矩阵: unmatched_trackers
  • 第一次进来时，跟踪目标为 0 ，直接返回。
  • 计算检测框和估计框的 iou ，生成一个 [len(detections), len(trackers)] 大小的矩阵
  • linear_assignment: 使用 KM 算法计算匹配结果，将匹配结果保存到 matched_indices 中。
  • 记录未匹配的检测框及跟踪框，未匹配的检测框放入 unmatched_detections 中，表示有新的目标进入画面，要新增跟踪器跟踪目标；未匹配的跟踪框放入 unmatched_trackers 中，表示目标离开之前的画面，应删除对应的跟踪器
  • 将匹配成功的跟踪框放入 matches 中，要求 iou 大与设定的阈值。将低于该阈值的分别放入 unmatched_detections 和 unmatched_trackers 中。 
    def associate_detections_to_trackers(detections, trackers, iou_threshold=0.3):
  if (len(trackers) == 0) or (len(detections) == 0):
      return np.empty((0, 2), dtype=int), np.arange(len(detections)), np.empty((0, 5), dtype=int)

  iou_matrix = np.zeros((len(detections), len(trackers)), dtype=np.float32)
  for d, det in enumerate(detections):
      for t, trk in enumerate(trackers):
          iou_matrix[d, t] = iou(det, trk)

  result = linear_sum_assignment(-iou_matrix)
  matched_indices = np.array(list(zip(*result)))

  unmatched_detections = []
  for d, det in enumerate(detections):
      if d not in matched_indices[:, 0]:
          unmatched_detections.append(d)

  unmatched_trackers = []
  for t, trk in enumerate(trackers):
      if t not in matched_indices[:, 1]:
          unmatched_trackers.append(t)

  matches = []
  for m in matched_indices:
      if iou_matrix[m[0], m[1]] < iou_threshold:
          unmatched_detections.append(m[0])
          unmatched_trackers.append(m[1])
      else:
          matches.append(m.reshape(1, 2))
  if len(matches) == 0:
      matches = np.empty((0, 2), dtype=int)
  else:
      matches = np.concatenate(matches, axis=0)

  return matches, np.array(unmatched_detections), np.array(unmatched_trackers)
CATALOG
    FEATURED TAGS
    Linux 驱动 CentOS Glibc PAM ukey Makefile autoconf automake shadow yum Dbus SELinux SEAndroid eCryptfs 备份数据/修复系统 DeepLeaning AI IPFS 区块链 Object Detective Multi Object Tracker Transformer TPM 可信计算 remoteattest 远程证明 IMA 完整性度量 Object Detection Object Classification