1. 概述
当你改变试验中的模型结构或者超参数时,模型的在训练数据集上误差变小了,但它在测试数据集上确不一定减少误差。这就是本篇文章研究的内容。
2. 训练误差和泛化误差
训练误差指模型在训练数据集上表现出的误差;泛化误差指模型在任意一个测试数据样本上表现出的误差的期望,并常常通过测试是数据集上的误差来近似。计算上述两种误差可以使用损失函数,平方损失函数和交叉熵损失函数。机器学习应该注重降低泛化误差。
2. 模型选择
选择模型就是从同类模型中选择不同超参数的模型。比如可以选择不同隐藏层数、不同隐藏层的隐藏单元个数和激活函数。
2.1 验证数据集
我们可以预留一部分在训练数据集和测试数据集以外的数据进行模型选择,这部分数据集称为验证数据集。例如,我们可以从给定的训练集中随即选取一小部分作为验证数据集,而将剩下的部分作为真正的训练集。
2.2. K 折交叉验证
由于验证数据集不参与模型训练,当训练数据不够用时,预留大量的验证数据实在太奢侈,一种改善的方案是 K 折交叉验证。我们把原始训练集分割成 K 份不重合的子数据集,然后我们做 K 次模型训练和验证。每一次,我们使用一个子数据集验证模型,并使用其他 K-1 个子数据集来训练模型。在这 K 次训练和验证中,每次用来验证模型的子数据集都不同。最后,我们对这 K 次训练误差和验证误差分别求平均。
2.3. 欠拟合和过拟合
在模型训练中,经常出现欠拟合和过拟合两类问题。模型无法得到较低的训练误差,这种现象称为欠拟合;模型训练误差远小于它在测试集上的误差,这种现象称为过拟合。在应用中,我们要尽可能同时应对欠拟合和过拟合。本文重点介绍两个引起上述两个问题的因素,一是模型复杂度;另外是训练数据集大小。
2.3.1. 模型复杂度
一般来说高阶多项式比低阶多项式函数的复杂度更高,因此高阶多项式函数比低阶多项式函数更容易在相同训练数据集上得到更小的训练误差。给定训练数据集,模型复杂度和误差之间的关系通常如下图所示。对于给定训练数据集,如果模型复杂度过低容易出现欠拟合;如果模型复杂度过高,很容易出现过拟合。所以要想避免欠拟合和过拟合必须对给定数据集选择合适复杂度的模型。
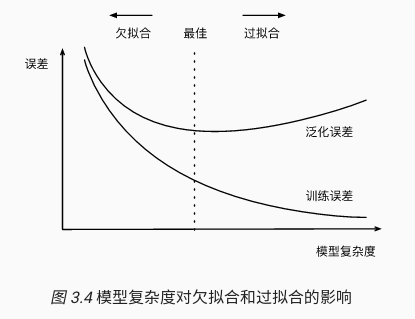
2.3.2. 训练数据集大小
一般来说如果训练数据集中样本数过少,特别是比模型参数数量更少时,过拟合更容易发生。此外,泛化误差会随着训练数据集里样本数量的增加而减小。因此在条件允许的情况下,我们尽可能的增大训练数据集,特别是模型复杂度更高的模型。
2.4. 欠拟合和过拟合示例
我们将使用人工生成的数据集。在训练数据集和测试数据集中,给定样本特征 x ,我们使用如下的三阶多项式函数来生成该样本的标签 y=1.2x−3.4x^2+5.6x^3+5+ϵ ,其中噪声 ϵ 项是服从均值为 0 ,标准差为 0.1 的正态分布。训练数据集和测试数据集的样本数都设为 100 。
正常情况下的,训练和测试拟合的曲线如下图所示,相关代码已上传到github
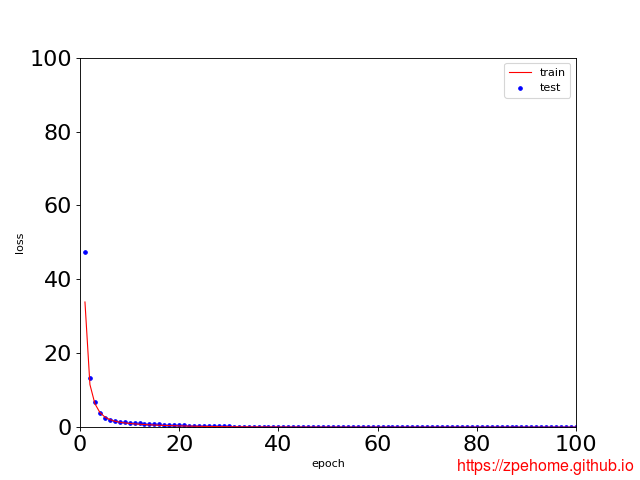
使用线性函数拟合,出现欠拟合现象,训练和测试拟合的曲线如下图所示,相关代码已上传到github
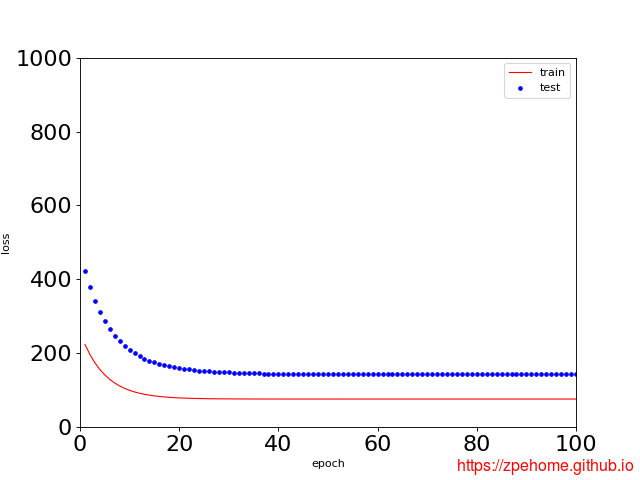
当样本数量不足时,出现过拟合现象,训练和测试拟合的曲线如下图所示,相关代码已上传到github
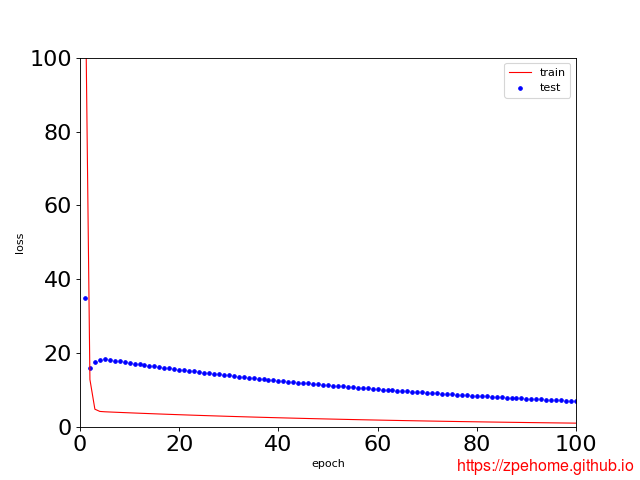
3. 权重衰减
上一节提到了防止过拟合现象产生的一个办法是增大训练数据集,但是获得额外的训练数据集往往代价极高。本节介绍应对过拟合的常用方法,权重衰减。
3.1. 方法
权重衰减等价于 L2 范数正则化。正则化通过为模型损失函数添加惩罚项使学习出的模型参数值较小,是应对过拟合的常用手段。
L2 范数正则化在模型原损失函数基础上添加 L2 范数惩罚项,从而得到训练所需要最小化的函数。 L2 范数惩罚项指的是模型权重参数每个元素的平方和与一个正数的乘积。以线性回归的损失函数为例,如下图所示:
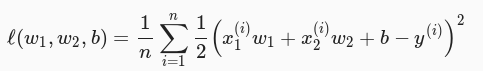
其中 w1 、 w2 是权重参数, b 是偏差参数,样本 i 的输入为 x1 、 x2 ,标签为 y ,样本数为 n 。将权重参数用向量 w = [w1, w2] 表示,带有 L2 范数惩罚项的新的损失函数为下图所示:
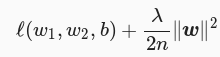
其中超参数 λ>0 。当权重参数均为 0 时,惩罚项最小。当 λ 较大时,惩罚项在损失函数中的比重较大,这通常会使学到的权重参数的元素较接近 0 。当 λ 设为 0 时,惩罚项不起作用。上式中 L2 范数平方 ∥w∥^2 展开后得到 w1^2+w2^2 。有了 L2 范数惩罚项后,在小批量随即梯度下降中,我们将线性回归中的权重迭代的方式变更为如下图所示:
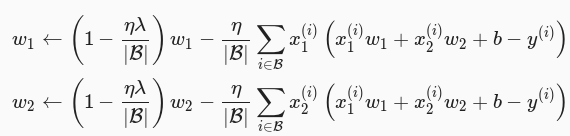
由上图可见, L2 范数正则化使权重 w1 、 w2 先乘以小于 1 的数,再减去不含惩罚项的梯度。因此 L2 范数正则化也叫权重衰减。权重衰减通过惩罚对值较大的模型参数为需要学习的模型增加了限制,这可能对过拟合有效。
3.2. L2 正则化示例
为了较容易地观察过拟合,我们考虑高维线性回归问题,如设维度p=200;同时,我们特意把训练数据集的样本数设低,如20。
我们假设要拟合的高维线性函数如下图所示:
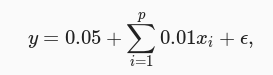
在不使用正则化的情况下,拟合的图像如下图所示,从下图可以明显的看出,训练误差远远小于测试误差。
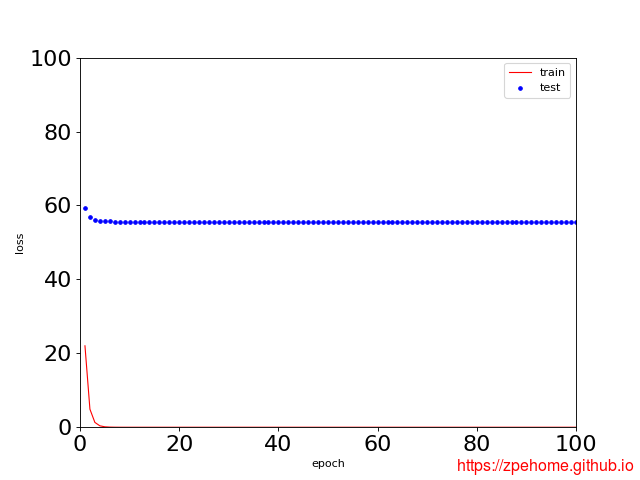
在使用权重衰减后,拟合的图像如下图所示,从下图可以看出,虽然训练误差有所增加,但测试集上的误差有所减少。另外,权重参数的L2范数比不使用权重衰减时的更小,此时的权重参数更接近0。
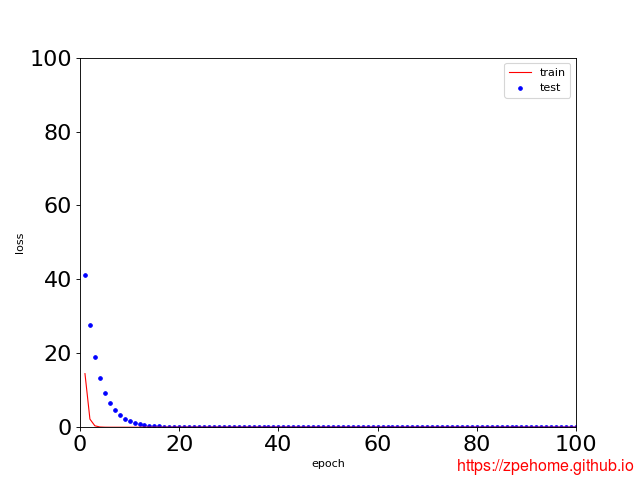
代码已上传到github
4. 丢弃法
除了上一节介绍的权重衰减外,丢弃法也是常用应对过拟合的方法。丢弃法通常是对输入层或隐藏层做如下操作:
- 随即选择一部分该层的输出作为丢弃元素
- 把丢弃元素乘以 0
- 把非丢弃元素拉伸
在集成学习里,我们可以对训练数据集有放回地采样若干次,并训练若干个不同的分类器;测试时,把这些分类器的结果集成在一起作为最终分类结果。丢弃法模拟集成学习,实质上是对每一个这样的数据集分别训练一个原神经网络子集的分类器。与一般的集成学习不同,这里每个神经网络子集的分类器使用同一套参数。使用丢弃法的神经网络实质上是对输入层和隐藏层的参数做了正则化,学到的参数使得原神经网络不同子集在训练数据上都尽可能表现良好。
丢弃法示例已上传到github上。