1. 概述
前两篇文章介绍的线性回归和 softmax 回归都是单层神经网络模型,但实际上深度学习更关注多层模型,尤其是卷积神经网络的出现。本篇文章以多层感知机 (multi-layer perception, MLP) 为例,介绍多层神经网络的概念。
2. 隐藏层
多层感知机在单层神经网络的基础上引入了一到多个隐藏层 (hidden layer) 。隐藏层位于输入层和输出层之间。下图展示了一个多层感知机含有一个隐藏层和 5 个隐藏单元:
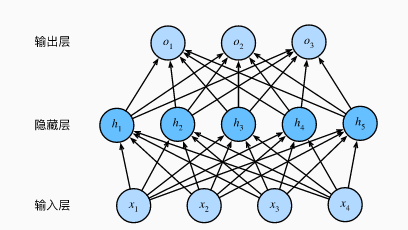
上图是一个层数为 2 的多层感知机,隐藏层中的神经网络和输入层各个输入完全连接,输出层的神经网络和隐藏层中的各个神经元也完全连接,所以多层感知机中的隐藏层和输出层都是全连接层 (full connection) 。虽然神经网络引入了隐藏层,却依然等价于一个单层神经网络,其输出为隐藏层的权重乘以输出层的权重。也就是说即使再多的隐藏层,以上设计依然只能与仅含输出层的单层神经网络等价。
3. 激活函数
上文提到,即使再多的隐藏层,以上设计依然只能与仅含输出层的单层神经网络等价。问题原因在于全连接层只对数据做仿射变换,而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换。例如对隐藏变量使用按元素运算的非线性函数进行变换,然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数。简单理解就是,复杂的分类器不能通过一条直线将各个类别划分开来,你可能需要使用一条弯曲的曲线将各个类别进行划分,这里的曲线就需要使用非线性激活函数将线性模型掰弯。
3.1. ReLU 激活函数
ReLU (rectified linear unit) 函数提供一个很简单的非线性变换,该函数只保留正数元素,并将负数元素清零。定义如下:
ReLU(x) = max(x,0)
ReLU 函数的曲线如下图所示,从下图可以看出 ReLU 保留正数元素,并将负数元素清零。
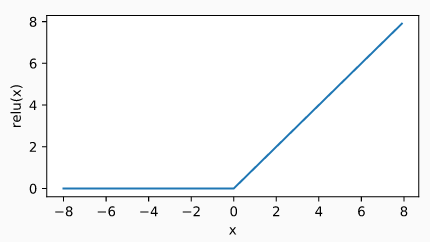
显然,当输入为负数时, ReLU 函数的导数为 0 ;当输入为正数时, ReLU 函数的导数为 1 。尽管输入为 0 时 ReLU 函数不可导,但是我们可以取此处的导数为 0 。 ReLU 函数的导数曲线如下图所示:
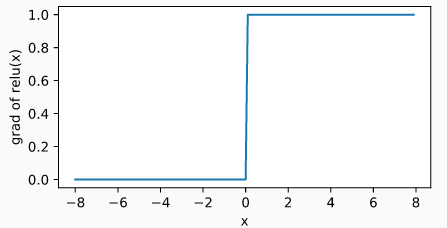
3.2. sigmoid 函数
sigmoid 函数可以将元素的值变换到 0 和 1 之间,定义如下:
sigmoid(x) = 1/(1 + exp(-x))
sigmoid 函数在早期的神经网络中较为普遍,目前已经逐步被 ReLU 函数取代。但是我们可以利用 sigmoid 函数的值域在 0 到 1 之间的这个特性来控制信息在神经网络中的流动。 sigmoid 函数曲线如下所示,当输入接近于 0 时, sigmoid函数越接近线性变换。
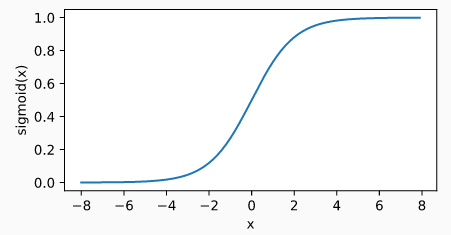
sigmoid 函数的导数定义如下:
sigmoid'(x) = sigmoid(x)(1 - sigmoid(x))
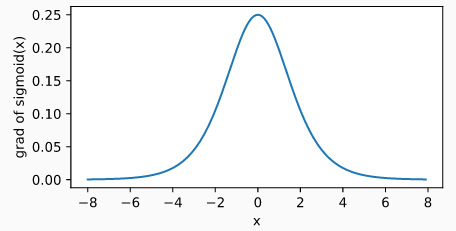
sigmoid 函数的导数如下如所示,当输入为 0 时, sigmoid 函数的导数达到最大值 0.25 ,当输入越偏离 0 时, sigmoid 函数的导数越接近 0 。
3.3. tanh 函数
tanh 函数,又称双曲正切函数,该函数可以将元素的值变换到 -1 到 1 之间。 tanh 函数定义如下:
tanh(x) = (1 - exp(-2x))/(1 + exp(-2x))
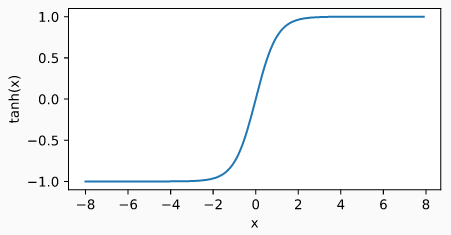
tanh 函数的曲线如下图所示,当输入接近 0 时, tanh 函数接近线性变换。 tanh 函数和 sigmoid 函数的曲线很像,但 tanh 函数在坐标系的原点上对称。
tanh 函数的导数定义如下:
tanh'(x) = 1 - tanh^2(x)
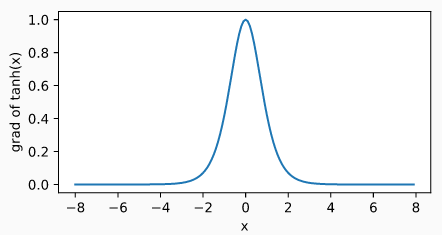
tanh 函数的导数如下图所示,当输入为 0 时, tanh 函数的导数达到最大值 1 ;当输入偏离 0 时, tanh 函数的导数趋近于 0 。
4. 多层感知机
多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络,且每个隐藏层的输出都通过激活函数进行变换。多层感知机的层数和各个隐藏层中隐藏单元个数都是超参数。
5. 实践
TensorFlow 实现 2 层神经网络训练手写识别训练集,代码已上传到github
MxNet 实现 2 层神经网络训练 mnist-fashion 训练集,代码已上传到github