1. 概述
线性回归模型适用于输出值为连续值的场景。那么,像图像分类这种输出为离散值的模型就不能使用线性模型进行训练。我们可以使用诸如 softmax 回归在内的分类模型。与线性回归不同, softmax 回归的输出单元为多个值,并且 softmax 运算使输出更适合离散值的预测和训练。
2. 分类问题
假设输入图像的高和宽均为 2 个像素,色彩为灰度。训练数据集中图像的真实标签为狗、猫或鸡,这些标签分别对应离散值 y1 、 y2 、 y3 。
通常我们使用离散的数值来表示类别,例如 y1=1 、 y2=2 、 y3=3 。这样,一张图像的标签为 1 、 2 和 3 这 3 个数值中的一个。虽然仍然可以使用回归模型来进行建模,并将预测值就近定点化到 1 、 2 和 3 这 3 个离散值之一,但这种连续值到离散值的转化通常会影响到分类质量。因此我们一般使用更加适合离散值输出的模型来解决分类问题。
3. softmax 回归模型
softmax 回归跟线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于, softmax 回归的输出值个数等于标签里的类别数。因为一共有 4 种特征和 3 种输出动物类别,所以权重包含 12 个标量、偏差包含 3 个标量,且对每个输入计算 o1 、 o2 、 o3 这 3 个输出,如下图所示:
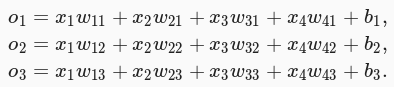
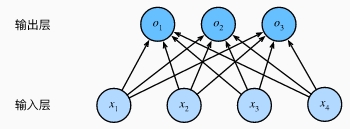
softmax回归同线性回归一样,也是一个单层神经网络。由于每个输出o1,o2,o3的计算都要依赖于所有的输入x1,x2,x3,x4,softmax回归的输出层也是一个全连接层。
4. softmax 运算
既然分类问题需要得到离散的预测输出,一个简单的办法是将输出值 o 当作预测类别是 i 的置信度,并将值最大的输出所对应的类作为预测输出,即输出 argmax(o) 。例如,如果 o1 , o2 , o3 分别为 0.1 , 10 , 0.1 ,由于 o2 最大,那么预测类别为 2 ,其代表猫。
然而,直接使用输出层的输出有两个问题。一方面,由于输出层的输出值的范围不确定,我们难以直观上判断这些值的意义。例如,刚才举的例子中的输出值 10 表示“高置信度”,图像类别为猫,因为该输出值是其他两类的输出值的 100 倍。但如果 o1=o3=1000 ,那么输出值 10 却又表示图像类别为猫的概率很低。另一方面,由于真实标签是离散值,这些离散值与不确定范围的输出值之间的误差难以衡量。
softmax 运算符(softmax operator)解决了以上两个问题。它通过下式将输出值变换成值为正且和为 1 的概率分布:
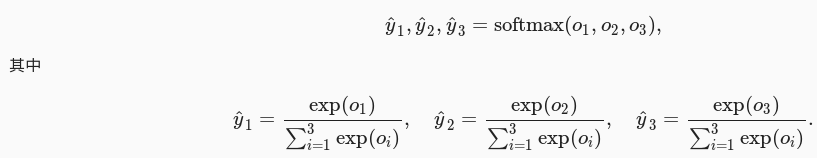
从上图可以看出 y^1+y^2+y^3=1 且 0≤y^1,y^2,y^3≤1 ,因此 y^1 , y^2 , y^3 是一个合法的概率分布。这时候,如果 y^2=0.8 ,不管 y^1 和 y^3 的值是多少,我们都知道图像类别为猫的概率是 80% 。此外,我们注意到 argmax(o)=argmax(y^) ,因此 softmax 运算不改变预测类别输出。
5. 交叉熵损失函数
前面提到,使用 softmax 运算后可以更方便地与离散标签计算误差。我们已经知道, softmax 运算将输出变换成一个合法的类别预测分布。实际上,真实标签也可以用类别分布表达:对于样本 i ,我们构造向量 y(i)∈Rq ,使其第 y(i)(样本 i 类别的离散数值)个元素为1,其余为0。这样我们的训练目标可以设为使预测概率分布 y^(i) 尽可能接近真实的标签概率分布 y(i) 。
我们可以像线性回归那样使用平方损失函数。然而,想要预测分类结果正确,我们其实并不需要预测概率完全等于标签概率。例如,在图像分类的例子里,如果 y(i)=3 ,那么我们只需要 y^(i)3 比其他两个预测值 y^(i)1 和 y^(i)2 大就行了。即使 y^(i)3 值为 0.6 ,不管其他两个预测值为多少,类别预测均正确。而平方损失则过于严格,例如 y^(i)1=y^(i)2=0.2 比 y^(i)1=0,y^(i)2=0.4 的损失要小很多,虽然两者都有同样正确的分类预测结果。
改善上述问题的一个方法是使用更适合衡量两个概率分布差异的测量函数。其中,交叉熵(cross entropy)是一个常用的衡量方法:
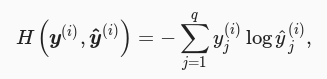
其中带下标的 y(i)j 是向量 y(i) 中非 0 即 1 的元素,需要注意将它与样本 i 类别的离散数值,即不带下标的 y(i) 区分。样本 i 中的离散值个数为 q ,分别代表 q 种类别的概率。在上式中,我们知道向量 y(i) 中只有第 y(i) 个元素 y(i)y(i) 为 1 ,其余全为 0 ,于是上图的公式可以简写成如下所示:
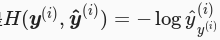
也就是说,交叉熵只关心对正确类别的预测概率,因为只要其值足够大,就可以确保分类结果正确。当然,遇到一个样本有多个标签时,例如图像里含有不止一个物体时,我们并不能做这一步简化。但即便对于这种情况,交叉熵同样只关心对图像中出现的物体类别的预测概率。交叉熵刻画的是两个概率分布之间的距离,或可以说它刻画的是通过概率分布q来表达概率分布p的困难程度,p代表正确答案,q代表的是预测值,交叉熵越小,两个概率的分布约接近。
6. 模型预测及评价
在训练好 softmax 回归模型后,给定任一样本特征,就可以预测每个输出类别的概率。通常,我们把预测概率最大的类别作为输出类别。如果它与真实类别一致,说明这次预测是正确的。我们将使用准确率(accuracy)来评价模型的表现,它等于正确预测数量与总预测数量之比。
7. 模型实现
7.1. softmax 运算实现
假设矩阵 X 的行数是样本数,列数是输出个数。为了表达样本预测各个输出的概率, softmax 运算会先通过 exp 函数对每个元素做指数运算,再对 exp 矩阵同行元素求和,最后令矩阵每行各元素与该行元素之和相除。这样一来,最终得到的矩阵每行元素和为 1 且非负。因此,该矩阵每行都是合法的概率分布。 softmax 运算的输出矩阵中的任意一行元素代表了一个样本在各个输出类别上的预测概率。代码实现如下所示:
def softmax(X):
X_exp = X.exp()
partition = X_exp.sum(axis=1, keepdims=True)
return X_exp / partition
7.2. softmax 模型定义
模型定义如下:
def net(X):
return softmax(nd.dot(X, W) + b)
7.3. 损失函数实现
为了得到标签的预测概率,我们可以使用 numpy 的 choose 函数。在下面的例子中,变量 y_hat 是 2 个样本在 3 个类别的预测概率,变量 y 是这 2 个样本的标签类别。通过使用 choose 函数,我们得到了 2 个样本的标签的预测概率。
y_hat = np.array([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y = np.array([0, 2], dtype='int32')
np.choose(y, y_hat.T)
那么交叉熵损失函数可以表示为:
def cross_entropy(y_hat, y):
return -np.choose(y, y_hat.T).log()
7.4. 计算分类精度
给定一个类别的预测概率分布 y_hat ,我们把预测概率最大的类别作为输出类别。如果它与真实类别 y 一致,说明这次预测是正确的。分类准确率即正确预测数量与总预测数量之比。
下面定义准确率 accuracy 函数
def accuracy(y_hat, y):
return (y_hat.argmax(axis=1) == y.astype('float32')).mean().asscalar()
7.5. 训练模型
mnist fashion 数据集格式如下图所示:
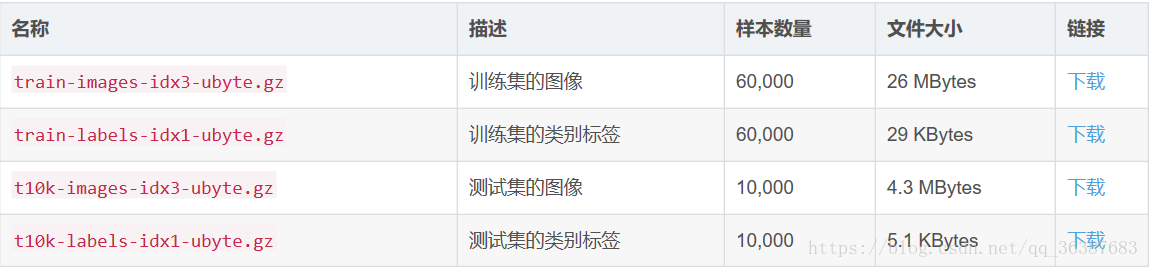
mnist 手写数字识别数据集格式如下图所示:
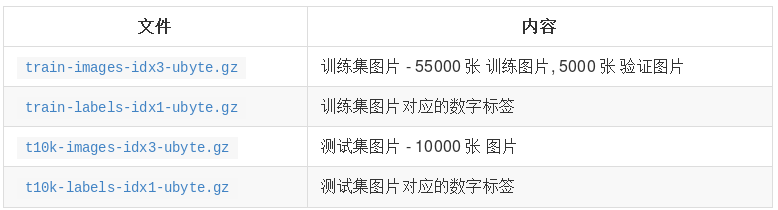
mxnet 手写识别实现代码已上传到github
mxnet fashion 识别实现代码已上传到github
mxnet fashion 识别自己实现的 load_data 获取数据集函数实现代码已上传到github
tensorflow 手写识别实现代码已上传到github
tensorflow fashion 识别实现代码已上传到github
tensorflow fashion 识别自己实现的 load_data 获取数据集函数实现代码已上传到github
在训练中发现我自己写的 load_data 获取数据集的函数,在训练时不收敛,定位发现是因为图像像素没有归一化导致。 mxnet 和 tensorflow 的现象不太一样,在没有归一化的请况下, tensorflow 压根不收敛,学习精确度一直是 0.1 , 归一化后 tensorflow 也能正常收敛,精度两个平台差不多。
图像归一化有如下好处:
- 转换成标准模式,防止仿射变换的影响。
- 减小几何变换的影响。
- 加快梯度下降求最优解的速度。
常见的归一化方法就是对训练数据集的像素数据除以 255 ,实现 [0, 1] 的归一化。