1. 概述
输出值为一个连续值的函数或模型称为线性回归。回归问题很常见,比如气温、房价等。
2. 基本要素
我们以预测房价为例。影响房屋价格的因素有很多,比如:面积和房龄。那麽房价与这两个因素到底有什么关系呢?
2.1. 模型
设房屋面积为 x1 ,房龄为 x2 ,房价为 y 。我们需要建立基于输出 x1 和 x2 来计算输出 y 的函数表达式,即模型。线性回归假设输出与输入之间的关系是线性关系:
yhat = x1w1 + x2w2 + b
其中 w1 和 w2 是权重(weight), b 为偏差(bias),且均为标量。他们是线性回归模型的参数。模型输出 yhat 是线性回归对真实价格 y 的预测或估计。他们之间通常存在一定的误差。
2.2. 训练数据
我们通常收集多套房子的真实价格和它们对应的面积和房龄数据。我们希望在这个数据上面寻找模型参数来使模型的预测价格与真实价格误差尽可能的小。在机器学习术语里,这些数据成为训练集(training set),一套房屋被称为一个样本(sample),其真实售价叫做标签(label),用来预测标签的两个因素叫做特征(feature)。特征用来表示样本的特点。
2.3. 损失函数
在模型训练中,我们需要衡量预测值与真实值的误差。通常选取一个非负数作为误差,且数据值越小误差越小。常用的方法是平方函数,如下图所示。
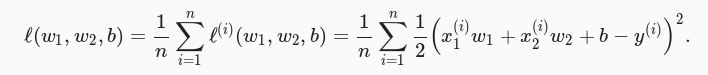
其中常数项 1/2 使对平方项求导数后的常数系数为1。这样在形式上简化了操作。显然误差越小表示预测价格与真实价格越接近,且当二者相等时误差为 0 。给定训练数据集,这个误差只与模型参数相关,因此我们将它记为以模型参数为参数的函数。在机器学习里,将衡量误差的函数成为损失函数(loss function)。这里使用的平方误差函数称为平方损失(square loss)。在模型训练中,我们希望找到一组参数,使训练样本的平均损失最小。
2.4. 优化函数
当模型和损失函数形式较为简单时,上面的误差最小化问题的解可以直接用公式表达出来。这类解叫作解析解(analytical solution)。本节使用的线性回归和平方误差刚好属于这个范畴。然而,大多数深度学习模型并没有解析解,只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。这类解叫作数值解(numerical solution)。
求数值解的优化算法中,小批量随机梯度下降(mini-batch stochastic gradient descent)在深度学习中被广泛使用。它的算法很简单:先选取一组模型参数的初始值,如随机选取;接下来对参数进行多次迭代,使每次迭代都可能降低损失函数的值。在每次迭代中,先随机均匀采样一个由固定数目训练数据样本所组成的小批量(mini-batch)B,然后求小批量中数据样本的平均损失有关模型参数的导数(梯度),最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。
在训练本节讨论的线性回归模型的过程中,模型的每个参数将作如下迭代:
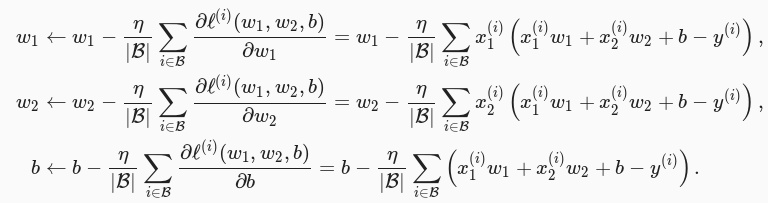
在上式中,B代表每个小批量中的样本个数(批量大小,batch size),η称作学习率(learning rate)并取正数。需要强调的是,这里的批量大小和学习率的值是人为设定的,并不是通过模型训练学出的,因此叫作超参数(hyperparameter)。我们通常所说的“调参”指的正是调节超参数,例如通过反复试错来找到超参数合适的值。
2.5. 模型预测
模型训练完成后,我们将模型参数 w1 、 w2 、 b 在优化算法停止时的值分别记作 w^1 、 w^2 、 b^ 。这里并不一定是最小化损失函数的最优解,而是对最优解的一个近似。然后,我们就可以使用学出的线性回归模型 x1w^1+x2w^2+b^ 来估算训练数据集以外任意一栋面积为 x1 、房龄为 x2 的房屋的价格了。这里的估算也叫作模型预测、模型推断或模型测试。
3. 模型实现
3.1. TensorFlow 实现
导入相关包:
import tensorflow as tf
import numpy as np
生成模型数据:
# 使用 NumPy 生成假数据(phony data), 总共 100 个点.
# np.random.rand 生成 2 行 100 列,取自[0,1)上的均匀分布
x_data = np.float32(np.random.rand(2, 100))
y_data = np.dot([0.100, 0.200], x_data) + 0.300
构建模型:
# 构造一个线性模型
b = tf.Variable(tf.zeros([1]))
W = tf.Variable(tf.random_uniform([1,2], -1.0, 1.0))
y = tf.matmul(W, x_data) + b
定义损失函数:
# 最小化方差
loss = tf.reduce_mean(tf.square(y - y_data))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
训练:
# 初始化变量
init = tf.global_variables_initializer()
# 启动图 (graph)
sess = tf.Session()
sess.run(init)
# 拟合平面
for step in range(0, 201):
sess.run(train)
if step % 20 == 0:
print(step, sess.run(W), sess.run(b))
# 得到最佳拟合结果 W: [[0.100 0.200]], b: [0.300]
代码地址 github 。
3.2. mxnet 实现
导入相关包:
from mxnet import autograd, nd
from mxnet.gluon import data as gdata
from mxnet.gluon import nn
from mxnet import init
from mxnet.gluon import loss as gloss
from mxnet import gluon
生成模型数据:
num_imputs = 2
num_examples = 1000
true_w = [5.6, -8]
true_b = 2.5
featrues = nd.random.normal(scale=1, shape=(num_examples, num_imputs))
lables = true_w[0] * featrues[:, 0] + true_w[1] * featrues[:, 1] + true_b
lables += nd.random.normal(scale=0.1, shape=lables.shape)
batch_size = 10
datasize = gdata.ArrayDataset(featrues, lables)
# shuffle=True 随机读取
data_iter = gdata.DataLoader(datasize, batch_size, shuffle=True)
构建模型:
# 定义模型
net = nn.Sequential()
# Dense:全连接层
# 1:该层输出个数
# 在 Gluon 中我们无须指定每一层输入的形状,例如线性回归的输入个数。
# 当模型得到数据时,例如后面执行 net(X) 时,模型将自动推断出每一层的输入个数。
net.add(nn.Dense(1))
# 初始化模型参数
net.initialize(init.Normal(sigma=0.01))
定义损失函数:
# 定义损失函数
# 平方损失又称L2范数损失
loss = gloss.L2Loss()
# 定义优化算法
# 小批量随机梯度下降
trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate' : 0.03})
训练:
# 训练模型
num_epochs = 3
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
# 为了减少计算和内存开销,默认条件下 MXNet 不会记录用于求梯度的计算。
# 我们需要调用 record 函数来要求 MXNet 记录与求梯度有关的计算。
with autograd.record():
l = loss(net(X), y)
# 对模型参数求梯度
l.backward()
# step函数来迭代模型参数
trainer.step(batch_size)
# 计算当前训练得到的参数对应的损失
l = loss(net(featrues), lables)
print('epoch %d, loss:%f' % (epoch, l.mean().asnumpy()))
dense = net[0]
print(true_w)
print(dense.weight.data())
print(true_b)
print(dense.bias.data())
代码地址 github 。